这是一个创建于 1455 天前的主题，其中的信息可能已经有所发展或是发生改变。
背景
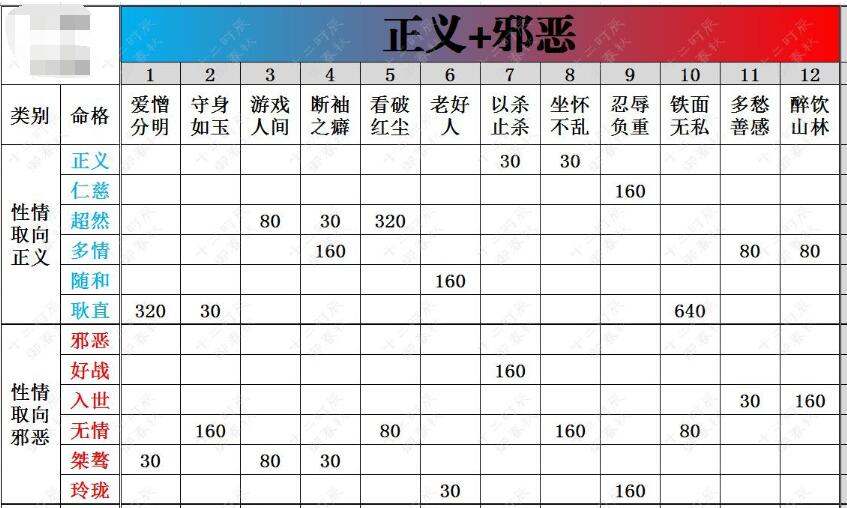
朋友在玩一个手游，里面有正邪 2 种性格设定，正邪性格内各分为 6 种命格，正邪内对应命格不能同时存在(如下图正义和邪恶不能同时存在)，但可以将一种命格清 0 积累相反的命格点数，命格点数到了之后可以换相应的称谓，要算出拿到以下所有称号需要的最短时间。
逻辑表达
- 存在 A,B,C,D,E,F 六种正义属性和 A',B',C',D',E',F'六种邪恶属性，每种属性有一定的属性值;
- A 和 A'不能同时存在（其余属性同理），但可以将 A 转换为 A'，但转换过会属性值会变为 0;
- 每天每种属性都可以加 10 点，也可以不加。相反属性允许同时相加，如给 A 加了 10 点属性值，A'再加 10 点等于给 A 减了 10 点属性值;
- 初始状态为邪恶属性值全满，可以理解为邪恶属性初始值无限大;
- 需要的称号如上图所示;
当前思路
没有思路，感觉上可以抽象成点到点的最短路径问题，但因为有转换清 0 的存在好像又不是这样=。=
第 1 条附言 · 2020-11-16 09:57:46 +08:00
逻辑表述重新编辑下：
- 存在 A,B,C,D,E,F 六种正义属性和 A',B',C',D',E',F'六种邪恶属性，每种属性有一定的属性值;
- A 和 A'不能同时存在（其余属性同理），属性值可以主动清0，可以用于为相反属性增加属性值；
- 每天每种属性都可以加 10 点，也可以不加。
- 初始状态为邪恶属性值全满，可以理解为邪恶属性初始值无限大;
- 需要的称号如上图所示，只要属性值到达了称号要求的点数即可换取，换取称号后属性点数不变;
 |
1
lihongming 2020-11-16 02:01:57 +08:00 via iPhone
看得不是很明白，几个问题：
1 、称号所需的属性值，是必须为这个数值，还是可以超过？没有值的属性是不考虑，还是必须为 0 ？ 2 、相反的属性转换是什么意思？比如 A 本来有 100 点，转换成 A’以后，A’到底有 100 点还是 0 点？如果是 0 点的话，那第二条规则是不是可以描述为——各属性值可以主动清零？ 3 、每天每种属性可以加 10 点那条规则，如果 A 本来有 100 点，今天选择给 A’加 10 点，是不是会变成 A 剩 90 点？如果是的话，那第三条规则是不是可以描述为——每天可以选择给每对属性加减 10 点？ |
 |
2
binux 2020-11-16 04:18:50 +08:00 via Android
一共 12 个顶点，算两两间距离为转换时间，算最短路径
|
 |
3
ciddechan 2020-11-16 08:45:20 +08:00
Dijkstra ？
|
 |
4
asuka321 OP @lihongming
1. 可以超过，属性值到了就可以拿到称号，拿到后属性值不变 2. 是的，即属性值能主动清 0 3. 是的，可以选择减 10 点，但如果是为了加相反属性的点数，应该先请 0 再加比较好 我把题目描述做下修改，表述能相对清晰点 |
 |
6
qinyusen 2020-11-16 10:20:54 +08:00
最小费用最大流
|
 |
8
lijialong1313 2020-11-16 10:47:26 +08:00
12 维的空间数组？
例如爱憎分明可以表示为：a[][][][][-30][320]，守身如玉可表示为：a[][][][-160][][30] 就是求空间最短路 |
 |
9
Edward0Chan 2020-11-16 14:13:16 +08:00
@binux #2 不行吧，每个属性每天都可以+10，那就是同时走六条路。你说的是一条路的情况吧
|
|
10
Edward0Chan 2020-11-16 14:21:14 +08:00
称号对应的多个属性值 是 或还是与的关系啊？
也就是只要满足一个属性值就行，还是满足称号下的所有属性才行？ |
|
11
binux 2020-11-16 14:47:26 +08:00 via Android
@Edward0Chan 算两点间距离的时候，考虑前序就行了。
|
|
12
asuka321 OP |
Select Language