这是一个创建于 3323 天前的主题,其中的信息可能已经有所发展或是发生改变。
我发现 V 友很喜欢读和机器学习有关的文章,今天就再写一篇,希望各位海涵。
前言
Dynamic Time Warping ( DTW ),动态时间规整算法诞生有一定的历史了(日本学者 Itakura 提出),它出现的目的也比较单纯,是一种衡量两个长度不同的时间序列的相似度的方法。 DTW 应用也比较广,主要是在模板匹配中,比如说用在孤立词语音识别(识别两段语音是否表示同一个单词),手势识别,数据挖掘和信息检索等中。
一、 DTW 算法原理
在时间序列中,需要比较相似性的两段时间序列的长度可能并不相等,在语音识别领域表现为不同人的语速不同。而且同一个单词内的不同音素的发音速度也不同,比如有的人会把“ A ”这个音拖得很长,或者把“ i ”发的很短。另外,不同时间序列可能仅仅存在时间轴上的位移,亦即在还原位移的情况下,两个时间序列是一致的。在这些复杂情况下,使用传统的欧几里得距离无法有效地求的两个时间序列之间的距离(或者相似性)。
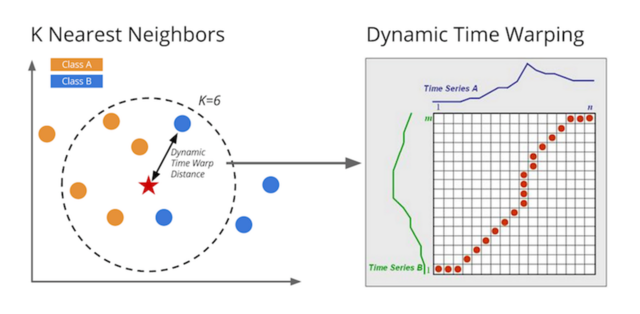
DTW 通过把时间序列进行延伸和缩短,来计算两个时间序列性之间的相似性:
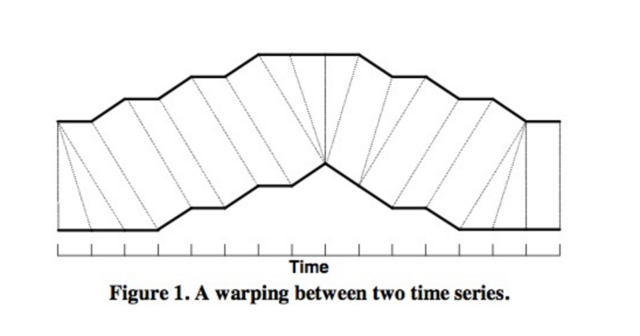
如上图所示,上下两条实线代表两个时间序列,时间序列之间的虚线代表两个时间序列之间的相似的点。 DTW 使用所有这些相似点之间的距离的和,称之为归整路径距离(Warp Path Distance)来衡量两个时间序列之间的相似性。
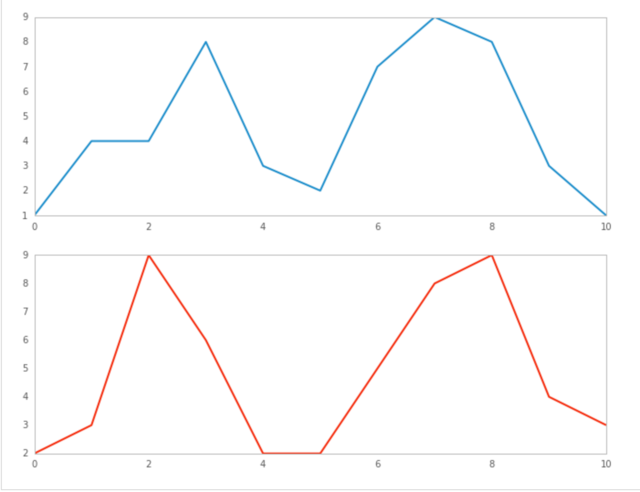
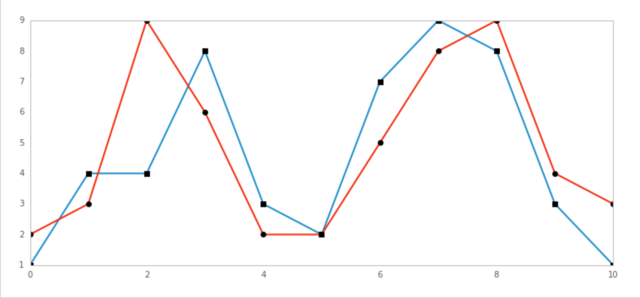
假设下图是两个不同主力期货合约的时间序列,在形态上非常相似,但是这些形态特征点(波峰、波谷)在时间上不能一一对齐,如果用基于欧氏距离的方法来计算两个序列的相似性,会不符合我们的直观认识。但如果匹配时,在序列上容许时间上的伸缩变形,则如下图的对应结果,匹配效果会大大增强,动态时间规整模型提供的就是允许数据在时间轴上伸缩变形的匹配方式。
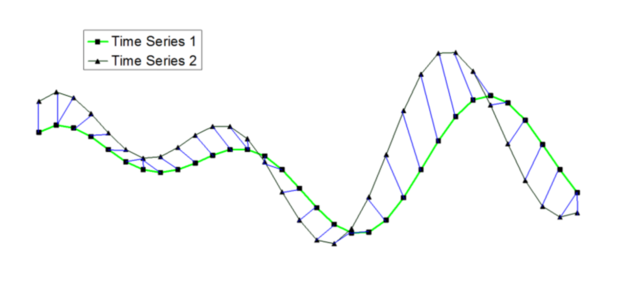
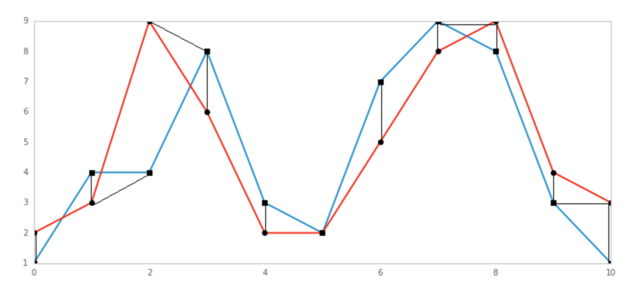
由下图可以看到,动态时间规整算法在进行两个序列匹配时,序列中的点不再是一一对应关系, 而是有一对一、一对多和多对一的不同映射。这种时间上的扭曲通过使得序列之间总体的距离最小化来实现。
具体而言,动态时间规整通过动态规划的方式来获得两个时间序列的时间对应关系,求得序列之间的最小距离。
二、 DTW 计算方法
假设两个多变量时间序列
X={x1,x2,⋯xm}
X={y1,y2,⋯ym}
和其中 X 含有 m 个观测样本, Y 含有 n 个观测样本,且每个观测样本 xi , i=1,2,…,m 和 yj , j=1,2,…,n 都是 q 维的多变量样本(维度一致)。在定义好多变量样本点 xi 和 yj 之间的距离计算方式 d ( xi , yi ) 之后,即可计算多变量序列 X 和 Y 的 动态时间规整距离
Distance(X,Y)=D(m,n)
DTW 计算步骤如下:
1 、将 i = 0 和 j = 0 时的 D ( i , j ) 值设置为正无穷大;
2 、对于 i 从 1 至 m , j 从 1 至 n ,通过迭代计算:
dij=d(xi,yj)
D(i,j)=dij+min{D(i−1,j),D(i,j−1),D(i−1,j−1)}
最终获得的 D(m,n) 即是多变量序列 X 和 Y 的动态时间规整距离。这是一个动态规划问题,可以通过 O ( mnq ) 次计算,获得两个多变量序列的最优匹配(其中 dij=d ( xi , yi ) 的计算复杂度为 O ( q ) 。
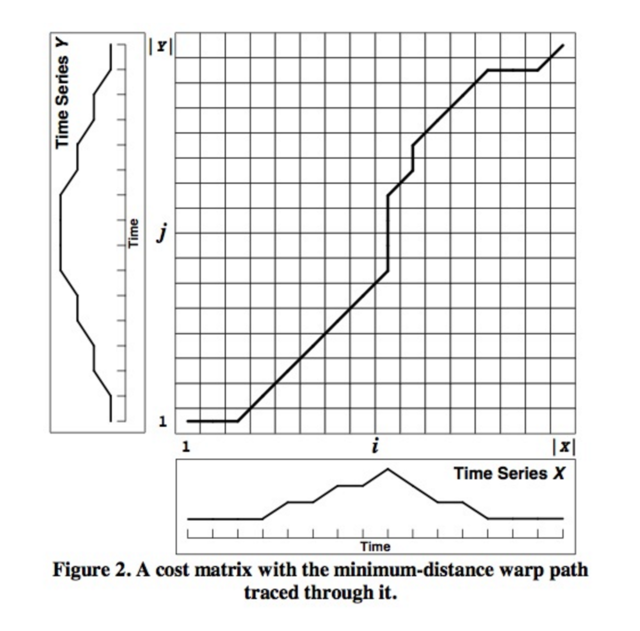
单步优化公式为:
D(i,j)=dij+min{D(i−1,j),D(i,j−1),D(i−1,j−1)}
其中, D ( i-1 , j ) 表示 xi-1 与 yj 匹配时的子序列距离, D ( i , j-1 ) 表示 xi 与 yj-1 匹配时的子序列距离, D ( i-1 , j-1 ) 表示 xi-1 与 yj-1 匹配时的子序列距离。动态时间规整算法从可能的三种拆分方式里边选择最优的一种,如图下图所示。
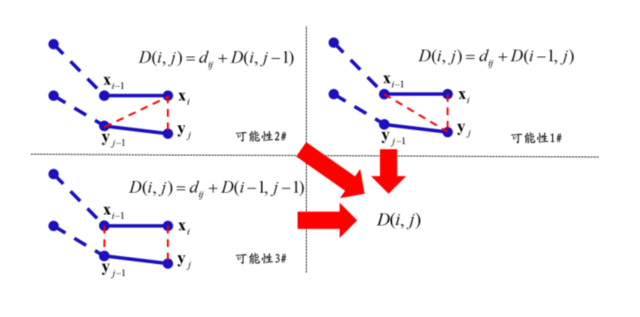
与之对比,普通的多变量匹配中不考虑时间的扭曲,因此要求两个序列等长,即 m=n ,计算复杂度为 O ( nq ) 。与普通的多变量时间序列匹配方法相比,动态时间规整可以获得更优的匹配效果,但是需要更长的计算时间。
在多变量时间序列中, xi 和 yj 都是 q 维的向量, 而且 xi 中的元素是时刻 i 下变量的值, yj 中的元素是时刻 j 下变量的值, d ( xi , yi ) 即是 i 时刻的 xi 和 j 时刻的 yj 对齐时的距离。向量 xi 和 yj 之间的距离计算方式 d ( xi , yi ) 可以通过欧氏距离或者马氏距离来计算,以单变量的序列为例
X={1,4,4,8,3,2,7,9,8,3,1}
Y={2,3,9,6,2,2,5,8,9,4,3}
定义
d(xi,yi)=∣∣xi−yi∣∣
通过动态时间规整计算两个序列的距离。
在这里要引入在 GitHub 的一位牛人,谷歌的数据科学家 Mark Regan 写的包
链接: K Nearest Neighbors & Dynamic Time Warping
K Nearest Neighbors & Dynamic Time Warping
When it comes to building a classification algorithm, analysts have a broad range of open source options to choose from. However, for time series classification, there are less out-of-the box solutions.
I began researching the domain of time series classification and was intrigued by a recommended technique called K Nearest Neighbors and Dynamic Time Warping. A meta analysis completed by Mitsa (2010) suggests that when it comes to timeseries classification, 1 Nearest Neighbor (K=1) and Dynamic Timewarping is very difficult to beat.
This repo contains a python implementation (and IPython notebook) of KNN & DTW classification algorithm.
以下是具体代码: https://uqer.io/community/share/57b81db5228e5b79a975a23f
导出图如下
三、 DTW 交易策略
采用日间的股指期货交易。第 t 个交易日的收盘价格和日成交量是一个观测样本
xt=(p(t),v(t))
需要通过模式识别对持仓至下一个交易日的收益率
rt=p(t+1)/p(t)−1
进行估计,以决定当日收盘时的建仓方向。
对于此前 L 个交易日的收盘价格和日成交量序列
Xt={xt−L+1,⋯xt−1,xt}
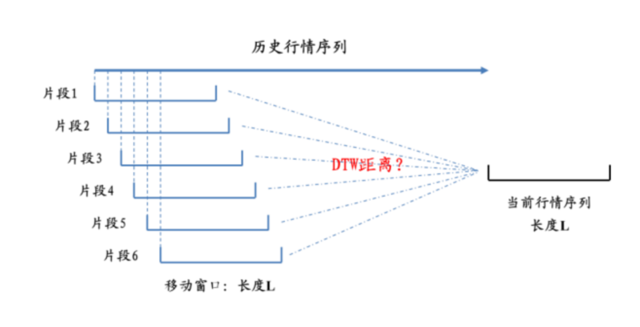
需要寻找与其相似的历史片段。首先,采用长度为 L 的移动窗口,将历史的行情划分为不同的行情片段,每一个片段为 L 个交易日的量价行情序列,如图下图所示。
由于篇幅有限,先转载到这里啦,余下的请看: https://uqer.io/community/share/57b81db5228e5b79a975a23f
前言
Dynamic Time Warping ( DTW ),动态时间规整算法诞生有一定的历史了(日本学者 Itakura 提出),它出现的目的也比较单纯,是一种衡量两个长度不同的时间序列的相似度的方法。 DTW 应用也比较广,主要是在模板匹配中,比如说用在孤立词语音识别(识别两段语音是否表示同一个单词),手势识别,数据挖掘和信息检索等中。
一、 DTW 算法原理
在时间序列中,需要比较相似性的两段时间序列的长度可能并不相等,在语音识别领域表现为不同人的语速不同。而且同一个单词内的不同音素的发音速度也不同,比如有的人会把“ A ”这个音拖得很长,或者把“ i ”发的很短。另外,不同时间序列可能仅仅存在时间轴上的位移,亦即在还原位移的情况下,两个时间序列是一致的。在这些复杂情况下,使用传统的欧几里得距离无法有效地求的两个时间序列之间的距离(或者相似性)。
DTW 通过把时间序列进行延伸和缩短,来计算两个时间序列性之间的相似性:

如上图所示,上下两条实线代表两个时间序列,时间序列之间的虚线代表两个时间序列之间的相似的点。 DTW 使用所有这些相似点之间的距离的和,称之为归整路径距离(Warp Path Distance)来衡量两个时间序列之间的相似性。
假设下图是两个不同主力期货合约的时间序列,在形态上非常相似,但是这些形态特征点(波峰、波谷)在时间上不能一一对齐,如果用基于欧氏距离的方法来计算两个序列的相似性,会不符合我们的直观认识。但如果匹配时,在序列上容许时间上的伸缩变形,则如下图的对应结果,匹配效果会大大增强,动态时间规整模型提供的就是允许数据在时间轴上伸缩变形的匹配方式。
由下图可以看到,动态时间规整算法在进行两个序列匹配时,序列中的点不再是一一对应关系, 而是有一对一、一对多和多对一的不同映射。这种时间上的扭曲通过使得序列之间总体的距离最小化来实现。
具体而言,动态时间规整通过动态规划的方式来获得两个时间序列的时间对应关系,求得序列之间的最小距离。

二、 DTW 计算方法
假设两个多变量时间序列
X={x1,x2,⋯xm}
X={y1,y2,⋯ym}
和其中 X 含有 m 个观测样本, Y 含有 n 个观测样本,且每个观测样本 xi , i=1,2,…,m 和 yj , j=1,2,…,n 都是 q 维的多变量样本(维度一致)。在定义好多变量样本点 xi 和 yj 之间的距离计算方式 d ( xi , yi ) 之后,即可计算多变量序列 X 和 Y 的 动态时间规整距离
Distance(X,Y)=D(m,n)
DTW 计算步骤如下:
1 、将 i = 0 和 j = 0 时的 D ( i , j ) 值设置为正无穷大;
2 、对于 i 从 1 至 m , j 从 1 至 n ,通过迭代计算:
dij=d(xi,yj)
D(i,j)=dij+min{D(i−1,j),D(i,j−1),D(i−1,j−1)}
最终获得的 D(m,n) 即是多变量序列 X 和 Y 的动态时间规整距离。这是一个动态规划问题,可以通过 O ( mnq ) 次计算,获得两个多变量序列的最优匹配(其中 dij=d ( xi , yi ) 的计算复杂度为 O ( q ) 。

单步优化公式为:
D(i,j)=dij+min{D(i−1,j),D(i,j−1),D(i−1,j−1)}
其中, D ( i-1 , j ) 表示 xi-1 与 yj 匹配时的子序列距离, D ( i , j-1 ) 表示 xi 与 yj-1 匹配时的子序列距离, D ( i-1 , j-1 ) 表示 xi-1 与 yj-1 匹配时的子序列距离。动态时间规整算法从可能的三种拆分方式里边选择最优的一种,如图下图所示。

与之对比,普通的多变量匹配中不考虑时间的扭曲,因此要求两个序列等长,即 m=n ,计算复杂度为 O ( nq ) 。与普通的多变量时间序列匹配方法相比,动态时间规整可以获得更优的匹配效果,但是需要更长的计算时间。
在多变量时间序列中, xi 和 yj 都是 q 维的向量, 而且 xi 中的元素是时刻 i 下变量的值, yj 中的元素是时刻 j 下变量的值, d ( xi , yi ) 即是 i 时刻的 xi 和 j 时刻的 yj 对齐时的距离。向量 xi 和 yj 之间的距离计算方式 d ( xi , yi ) 可以通过欧氏距离或者马氏距离来计算,以单变量的序列为例
X={1,4,4,8,3,2,7,9,8,3,1}
Y={2,3,9,6,2,2,5,8,9,4,3}
定义
d(xi,yi)=∣∣xi−yi∣∣
通过动态时间规整计算两个序列的距离。
在这里要引入在 GitHub 的一位牛人,谷歌的数据科学家 Mark Regan 写的包
链接: K Nearest Neighbors & Dynamic Time Warping
K Nearest Neighbors & Dynamic Time Warping
When it comes to building a classification algorithm, analysts have a broad range of open source options to choose from. However, for time series classification, there are less out-of-the box solutions.
I began researching the domain of time series classification and was intrigued by a recommended technique called K Nearest Neighbors and Dynamic Time Warping. A meta analysis completed by Mitsa (2010) suggests that when it comes to timeseries classification, 1 Nearest Neighbor (K=1) and Dynamic Timewarping is very difficult to beat.
This repo contains a python implementation (and IPython notebook) of KNN & DTW classification algorithm.

以下是具体代码: https://uqer.io/community/share/57b81db5228e5b79a975a23f
导出图如下



三、 DTW 交易策略
采用日间的股指期货交易。第 t 个交易日的收盘价格和日成交量是一个观测样本
xt=(p(t),v(t))
需要通过模式识别对持仓至下一个交易日的收益率
rt=p(t+1)/p(t)−1
进行估计,以决定当日收盘时的建仓方向。
对于此前 L 个交易日的收盘价格和日成交量序列
Xt={xt−L+1,⋯xt−1,xt}
需要寻找与其相似的历史片段。首先,采用长度为 L 的移动窗口,将历史的行情划分为不同的行情片段,每一个片段为 L 个交易日的量价行情序列,如图下图所示。

由于篇幅有限,先转载到这里啦,余下的请看: https://uqer.io/community/share/57b81db5228e5b79a975a23f
1
ob 2016-11-07 16:34:07 +08:00 via Android 好高深,留个爪。
|
2
Mac 2016-11-07 19:37:51 +08:00 先留个银子,我最近也被动态规划烦得要死,等有空看看思路
|
3
jedihy 2016-11-10 10:46:26 +08:00 这个 DTW 不就是一个简单的 DP 问题吗? Sequence Alignment 或者叫做 Edit Distance 。跟 DNA 找相似性的办法一模一样。
|
4
jedihy 2016-11-10 10:53:41 +08:00 DTW 有个缺陷,只能跟一只股票进行比较,如果跟 K 个股票比较的话时间复杂度是(2^K-1) * N^K ,假设长度都是 N 。看来 DNA 对齐的很多算法都可以拿来做股票分析啊,不知道用 progressive 或者 STAR 算法会有什么效果。
|